Laser Systems for Optical Microscopy
The lasers commonly employed in optical microscopy are high-intensity monochromatic light sources, which are useful as tools for a variety of techniques including optical trapping, lifetime imaging studies, photobleaching recovery, and total internal reflection fluorescence. In addition, lasers are also the most common light source for scanning confocal fluorescence microscopy, and have been utilized, although less frequently, in conventional widefield fluorescence investigations.
Lasers emit intense packets of monochromatic light that are coherent and highly collimated to form a tight beam with a very low rate of expansion. Compared to other light sources, the extremely pure wavelength ranges emitted by the laser have a bandwidth and phase relationship that is unparalleled by tungsten-halogen or arc-discharge lamps. As a result, laser light beams can travel over long distances and can be expanded to fill apertures or focused to a very small spot with a high level of brightness. Beyond the similarities common to all lasers, which include a gain medium (light source), excitation source (power supply), and resonator, these light sources differ radically in size, cost, output power, beam quality, power consumption, and operating life.
The coherence of monochromatic light produced by most laser systems introduces problems in the application of these light sources for classical widefield microscopy. Light scattering and diffraction patterns are introduced by interference at every surface in the optical path. In addition, the field and aperture diaphragms, as well as dirt, also produce artifacts. These undesirable effects can be minimized or eliminated by a variety of techniques. The most common methods include temporally scrambling laser light by rapidly varying the optical path length between the light source and the microscope, or scanning the specimen point by point as is the case in confocal microscopy systems. In addition, interference and other artifacts can often be eliminated by the aperture scanning technique. If the path length or coherence state of the laser beam fluctuates at a faster interval than the detector integration time (in effect, the video frame rate), the speckle and scattering artifacts disappear from the image.
A successful technique employed by some investigators to improve differential interference contrast (DIC) images produced with an argon ion laser light source is to position a circular glass wedge, spinning at 2500 revolutions per minute, in the light path. Rapid variations in optical path length are introduced by differences in wedge thickness as the wedge rotates in front of the expanded laser beam. Currently, path length variation is usually accomplished by employing a fiber-optic light pipe to route the light between the light source and the microscope. Vibrating the fiber produces continual changes in the optical path length, causing the beam to become temporally incoherent at frequencies below that of the vibration level. The vibrations may be generated by a piezoelectric device, a loudspeaker, or the cooling fan utilized in the laser head.
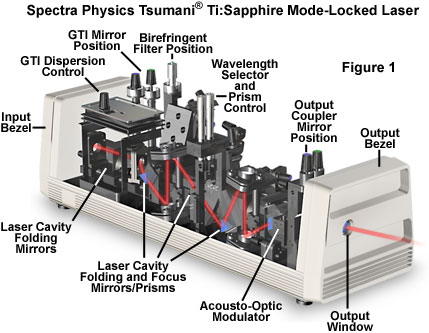
Illustrated in Figure 1 is a self mode-locked Ti:sapphire pulsed laser, which is currently one of the preferred laser excitation sources in a majority of multiphoton fluorescence microscopy investigations. Ti:sapphire mode-locked lasers provide a large wavelength tuning range, from about 690 to over 1050 nanometers, with pulse widths approximately 100 femtoseconds in length. In addition, these lasers have sufficient power (greater than 100 milliwatts throughout the tuning range) for saturation of two-photon excitation in most fluorophores. To ensure proper cooling and humidity control of the laser crystal, nitrogen gas is pumped into the sealed laser head, which is maintained at constant temperature by an external chiller.
The light produced by many laser systems is linearly polarized, with a polarization vector oriented vertically. This property can be exploited in applications requiring a polarized illumination source, such as differential interference contrast, polarized light measurements, or quantitative investigations of fluorescence polarization anisotropy.
The coherence and polarization characteristics of a laser beam are measured by the distribution of light in the beam cross-section, or profile, which changes with increasing distance from the exit mirror of the laser. The following discussion of laser beam characteristics is presented as a general overview of the subject that may prove useful in employing lasers in microscope imaging, laser trapping, and other applications.
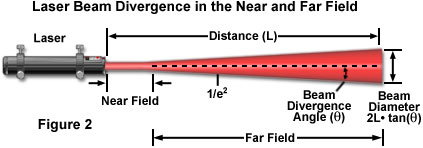
When a laser operates in the simplest transverse electromagnetic mode, referred to as the TEM(00) mode, the emitted beam has a planar wave front and a Gaussian intensity (irradiance) profile. The laser beam diameter is commonly defined as the value at which the intensity has fallen to e(E-2) (13.5 percent) of its peak value. The Gaussian profile of the laser beam arises because of diffraction, which prevents the propagation of a perfectly collimated beam and induces transverse spreading of the light waves. Near the laser output aperture (termed the near field), the phase fronts of the beam can become disordered. As a consequence, the beam cross-sectional shape, size, and irradiance profile then change rapidly with distance from the laser. At greater distances (the far field), the phase fronts stabilize into the resultant Gaussian profile. In some literature references, the near field and far field are referred to by the alternative terms of Fresnel zone and Fraunhofer zone, respectively. The near field is also sometimes termed the Rayleigh range. The far field begins at a distance, z, defined by
z = A02/λ
where A(0) is the beam diameter at the exit aperture and λ is the wavelength of light emitted by the laser. Applying this equation to an argon laser emitting a 0.6-millimeter-waist-diameter beam at a wavelength of 488 nanometers, the far field begins at approximately 74 centimeters from the exit aperture.
Presented in Figure 2 is a schematic diagram of laser beam geometry and divergence in the near and far fields. As discussed above, the beam can be considered essentially a parallel bundle of wavefronts that undergoes little spreading in the near field. Beyond the near field, the beam divergence angle (θ), which is measured from the center of the beam to the edge (e(E-2)), grows larger and becomes the critical parameter in determining beam diameter (D) according to the equation:
Beam Diameter (D) = 2L • tan(θ)
where D is the variable signifying laser beam diameter and L represents the length of the distance from the laser exit aperture to the measurement point on the beam. In practice, several laser beam characteristics, including the irradiance profile, are critical factors in many microscopy applications, and knowledge of the distance to the far field may be necessary in configuring the imaging system. Table 1 presents calculated values of this distance (using the equation given above) for a number of commonly utilized lasers and emission lines, and typical beam waist diameters.
Distance to the Far Field
| Wavelength (nm) | Beam Diameter (mm) | Far Field Distance (cm) |
| Argon-Ion | ||
| 488 | 0.6 | 74 |
| 514 | 1.0 | 195 |
| Helium-Neon | ||
| 543 | 0.4 | 30 |
| 594 | 0.7 | 83 |
| 612 | 0.7 | 80 |
| 632 | 0.7 | 78 |
| Nd:YAG | ||
| 355 | 3.0 | 2535 |
| 532 | 1.0 | 188 |
| Ti:Sapphire | ||
| 790 | 2.0 | 506 |
| 395 | 2.0 | 1012 |
| 790 | 0.8 | 81 |
Table 1
Whether or not the beam exhibits Gaussian character is important in most laser applications because the beam often has to be focused, shaped, and otherwise modified by lenses and other optical components. A Gaussian beam has certain definable transformation characteristics, and these enable assumptions to be made about how the beam will propagate through an optical system.
The angular radius (or beam divergence angle; see Figure 2), designated by θ (in radians), of a Gaussian beam in the far field is approximated by the expression:
θ = λ /πa0
where a(0) is the beam waist radius at the laser exit aperture. The beam waist diameter is a function of laser wavelength, cavity length, and other design parameters of the cavity. As the distance (z) from the laser increases, the beam waist radius is given by the equation:
a(z) = θz
Typically, laser beams are characterized by beam propagation parameters such as the square of M, or K (which is equivalent to the reciprocal of the square of M), determined from a combination of near field and far field measurements as follows:
M2 = πA0θ/4λ
Smaller values of M2, which is termed a propagation constant or propagation factor, are indicative of higher beam quality, particularly in reference to a smaller diameter and divergence. The factor describes the relationship of the real beam to that of an ideal Gaussian beam.
Coherent Gaussian beams have specific properties that cause them to differ from incoherent light beams in their propagation and transformation by lenses and mirrors. In the case of a diffraction-limited beam, the intensity profile of a Gaussian beam is itself Gaussian, provided that the beam is not truncated by the lens aperture. When the Gaussian beam diameter is one-half the aperture diameter of the lens, the intensity profile of the emergent beam remains Gaussian. When the Gaussian beam diameter is equal to the diameter of the lens aperture, the output beam intensity profile is a mixture of the Gaussian function and that of an Airy disk. Finally, a Gaussian beam diameter significantly larger than the diameter of the lens aperture produces the output profile of an Airy disk. In the latter instance, much of the laser power may be lost due to overfilling of the lens entrance aperture.
The overall topic of Gaussian beam optics is thoroughly covered in numerous textbooks, and details not discussed here may be obtained from more comprehensive sources. Two types of manipulation of the Gaussian beam are of particular interest to the microscopist utilizing lasers - beam concentration and beam expansion.
When a laser beam is focused to a very small spot by an aberration-free microscope objective (beam concentration), the radius of the spot at the focus (at distance z) is given by the expressions:
a(z) = λ
f/πa0
where f is the focal length of the lens. As an example, if a 100x objective having a numerical aperture of 1.3 (producing a focal length of approximately 1.6 millimeters) is employed to concentrate the 488-nanometer beam of an argon laser having a 0.3-millimeter radius, the focused spot radius (determined from the previous equation) is 0.8 micrometer. Increasing the beam waist fivefold through beam expansion (as discussed below) would result in a focused spot radius of approximately 0.16 micrometer.
It is important to note that extremely high power densities are achieved at the focal point of a concentrated laser beam. A 10-milliwatt beam focused to a diffraction-limited spot 0.22 micrometers in diameter results in a power density of approximately 30-million watts per square centimeter. Such high energy levels can rapidly degrade or destroy lens and filter coatings, as well as introduce considerable photochemical damage to biological specimens. However, for such a minute spot size, diffusion of thermal energy can be so effective in water that a high-energy, near-infrared beam may do little damage to a biological specimen unless absorption of the energy by the specimen is sufficiently high.
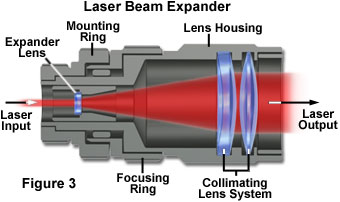
In many applications of lasers in optical microscopy, the laser beam is initially expanded by the use of a Keplerian or Galilean beam expander, either of which is actually a reversed telescope (typical laser beam expander anatomical features are illustrated in Figure 3). The divergence of a coherent Gaussian beam can be reduced, and the beam optimally collimated over a longer distance, if the laser beam is first expanded. Referring to the previous equations, the angular radius of the beam, designated θ, is inversely proportional to the beam waist radius, a(0), at the laser exit aperture. Therefore, expanding the beam waist radius diminishes the divergence proportionally.
It is practical for many applications in microscopy to pipe the laser output directly into the microscope optical path through a flexible optical fiber (as illustrated in Figure 4). This technique is preferable to the alternative method of rigidly aligning the laser and microscope, which requires employing a massive, vibration-free optical table and numerous fixed mirrors and other components.
When a laser beam is focused by a lens onto an optical fiber, the coupling efficiency and characteristics of the beam that emerges from the fiber depend heavily on the fiber geometry. Most of the optical fibers utilized for laser light delivery are constructed with a fused-silica core. These fibers consist of an inner core fabricated with high-refractive-index silica and surrounded by a sleeve, termed the cladding, composed of lower-refractive-index material. Light is prevented from escaping the fiber along its length by total internal reflection at the interface of the core and the cladding. The cladding may be composed of silica, glass, a hard fluoropolymer, or a soft silicone.
Optical fibers are classified as single-mode or multimode according to the diameter of their inner cores. A single-mode fiber allows propagation of only the lowest-order mode at one particular wavelength (Figure 4). The wavelength propagated and polarization preservation of the wave are determined by the fiber diameter. Although other wavelengths may propagate, they do so with reduced efficiency. Typical single-mode fiber diameters range from 3 to 6 micrometers for visible-light wavelengths, and the output irradiance profile of a single-mode fiber is Gaussian.
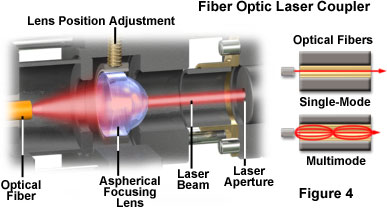
A multimode optical fiber enables the propagation of more than one mode, and is not restricted to a single wavelength. The inner cores of multimode optical fibers are larger than single-mode fibers, ranging from approximately 100 micrometers to 1.2 millimeters in diameter. The output irradiance profile from a multimode fiber has a flat shape, referred to as a top-hat profile, with a numerical aperture that is determined by the core and cladding refractive indices.
The acceptance cone angle, θ, of the fiber core is related to the numerical aperture, NA, of the fiber as follows:
NA = sin θ/(n2core - n2cladding)1/2
where n represents refractive index. Efficient coupling of laser light to the fiber core occurs when the fiber core numerical aperture and that of the beam concentration lens are matched. The efficiency of light transmission through an optical fiber is typically as high as approximately 90 percent, but may be sharply reduced (to only 60 or 70 percent) by bends having very small radii (less than 3 centimeters).
In utilizing any laser, it is crucial not only to prevent any direct or specularly reflected laser light from entering an observer's eyes, but also to avoid reflection of the beam from a component of the optical system back into the laser system. The former is an obvious personal safety precaution, while the latter caution is important to prevent an additional reflector from returning a coherent beam back into the laser, causing possible damage to the system.
Stability of the laser light source is an important aspect in many applications, particularly in quantitative microscopy, where illumination intensity fluctuations can adversely affect experimental results. A number of factors related to stimulated emission and cavity length fluctuations can induce frequency noise in the output beam, but other perturbations causing amplitude fluctuations can create both high-frequency intensity noise and slow variations (drift) in optical output power. Some sources of these intensity fluctuations are related to the function of the laser head itself or the power supply. The most common sources of noise in the output beam for various laser categories are listed below:
- Gas lasers - Mirror misalignments from resonator vibrations, noise from optical pump sources, plasma oscillations and instabilities of the ion discharge process, fluctuations in power supply current, microphonics from cooling water turbulence, and fan-induced noise in forced-air cooling systems are all potential noise sources.
- Solid-state lasers - Noise sources include microphonics, pump source fluctuations for both lamp and diode pumps, cavity alignment errors, and the random frequency-related noise (termed 1/fnoise) that is related to thermal fluctuations in the laser medium.
- Dye lasers - Both noise (high-frequency) and drift result from density inhomogeneity and air bubbles in the dye solution, and by dye pump and laser pump source instabilities.
- Semiconductor (diode) lasers - Noise can result from fluctuations in the drive (bias) current or temperature, and 1/f noise is caused by trapping of carriers in the junction and by other types of carrier (electron-hole) recombination effects.
All lasers are susceptible to noise introduced by their power supplies. Switching power supplies, which have become common because of their efficiency and small size, are particularly likely to introduce ripple to the laser system at frequencies ranging into the tens of kilohertz. Such interference, when it affects the light beam in optical microscopy systems, can be especially troublesome to diagnose and remove. The primary difficulty is due to the similarity with noise introduced into the system by other sources, such as electromagnetic fields in the laboratory environment. In order to achieve adequate output stability, semiconductor lasers must be operated with diode current supplies having the highest electrical stability and lowest noise available, and with precise temperature control. Other external noise sources must be controlled, including dust in the laboratory, and vibrations originating from local traffic and building equipment.
The beam intensity of continuous wave (cw) lasers can be stabilized by either electronic control of the tube current or through utilization of external components that modulate the light intensity. Two different methods are often employed to control the tube drive current. In the constant current mode, tube current is directly controlled by an electronic feedback loop to minimize fluctuations. Because the laser output is also temperature dependent, this type of control circuit is most effective if adequate temperature control is provided. Constant output power stabilizing systems operate by controlling the drive current in response to a signal derived from a circuit that samples the output beam using a beamsplitter and photodiode monitor. This physical arrangement is applicable for gas lasers and several other geometries, but smaller diode lasers are commonly assembled in a package that already includes an integral photodiode. The monitor photodiode samples emission from the rear facet of the laser wafer and produces a signal that enables feedback control of the output power.
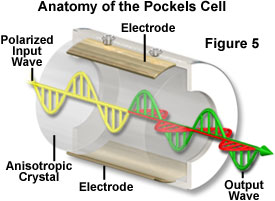
External components utilized to provide stabilization of laser intensity generally employ a fast feedback system to control an electro-optic modulator that minimizes fluctuations in beam power. The external Pockels cell modulator (see Figure 5) is available from a number of manufacturers, and can be used, in principle, to stabilize the output power of any continuous wave laser. Large intensity fluctuations (up to approximately 50 percent) can be corrected by this technique, but with a proportional reduction in total output power. A wide range of correction capability is important with many systems. The helium-cadmium laser, for example, can exhibit variation in output power of around 20 percent, due in part to strong plasma oscillation between certain beam frequencies. Systems exist that are reported to be suitable for regulating cw and mode-locked lasers to within a few hundredths of a percent of their output power, and over a frequency range from direct current to several hundred megahertz, with noise attenuation of 500:1, or greater.
The basic components of a Pockels cell modulator are presented in Figure 5. External devices for regulating laser output intensity, similar to the design illustrated in Figure 5, are sometimes categorized or marketed under the term noise eaters. The fundamental concept behind electro-optic modulators utilizing the Pockels effect is based on a mechanism for varying the polarization properties of the cell at an extremely rapid rate to provide a variable beam attenuator for control of laser intensity. The polarization state of the laser output determines the total attenuation of the modulator, but up to 80 percent transmission is possible. Following emission from the laser head, a portion of the beam is diverted by a beamsplitter to a photodiode, which compares the intensity to a preset (selectable) reference intensity, and amplifies the difference signal so that it can drive the electro-optic Pockels cell modulator. The amplified signal produces a refractive index change in the cell that rotates the plane of polarization, thereby varying the beam attenuation in proportion to the difference voltage that is applied. Among substances that exhibit a change in polarization properties with changes in electric field (Pockels effect) are potassium dihydrogen phosphate and lithium niobate, and crystals of these materials are commonly utilized in the beam modulators.
In situations where randomly polarized light is stabilized by a Pockels cell system, the modulator must be positioned between crossed polarizers, and further consideration is necessary to minimize the effects of these additional components on the beam stability. Because dust, vibrations, and other interferences can alter beam stability at any point in the optical path, it is important that external stabilizers are placed as close as possible to the specimen position in optical microscopy systems. This effort will ensure that the most stable beam is delivered to the specimen.
Both the argon-ion laser and krypton-ion laser produce multiple emission lines from rare-gas transitions that differ substantially in power levels, and only a few of the lines are suited for microscopy applications. The air-cooled argon-ion laser is widely employed as a light source for confocal microscopy because of its brightness level, small size, excellent beam geometry, and the suitability of its spectral lines for fluorescein and (less efficiently) rhodamine excitation. Most argon-ion lasers utilized in widefield or confocal fluorescence microscopy emit only two usable lines, 488 and 514.5 nanometers, which represent approximately 75 percent of the total laser power. Higher-power (greater than 5 watts) argon-ion lasers equipped with special mirrors can emit ultraviolet lines at 334, 351, and 364 nanometers, and additional lines at visible wavelengths extending from 458 to 529 nanometers.
Krypton-ion lasers have found fewer applications in microscopy than argon lasers due to their somewhat longer wavelength output. In addition, krypton produces only 10 to 30 percent as much power as argon when used in the same tube, and often requires water-cooling to generate the equivalent power output of an air-cooled argon system. A major drawback of air-cooled ion lasers is their lack of efficiency, which results in large power requirements and excessive heat generation that must be removed from the system by forced air with exhaust fans. The lifespan of ion lasers is reduced due to gas consumption, with trapped gas being buried within the walls of the discharge tube as a result of the high current densities necessary for laser operation.
Air-cooled lasers using argon-krypton mixtures have become popular in confocal microscopy when several illumination wavelengths are required for dual or multiple-fluorophore studies. Such mixed-gas lasers are only capable of producing stable output on major lines that are well separated in the wavelength spectrum. Of the three laser lines typically utilized for confocal microscopy, the 488-nanometer and 568-nanometer lines have approximately equal power (10 to 15 milliwatts), while the 647-nanometer line has about 50 percent more (15 to 25 milliwatts). All ion lasers exhibit excellent beam quality and can be purchased from a variety of manufacturers in single-line, multi-line, and tunable configurations.
The emission at 632 nanometers (termed the He-Ne line) of the common helium-neon laser has been supplemented by development of variants having emissions in the green (543 nanometers), yellow (594 nanometers), orange (612 nanometers), red (633 nanometers), and near infrared (1523 nanometers) spectral ranges. Although most of these lasers are single-line emitters and relatively low in power (less than 10 milliwatts), the helium-cadmium laser is an exception, emitting at 325 or 442 nanometers with greater than 50 milliwatts of power.
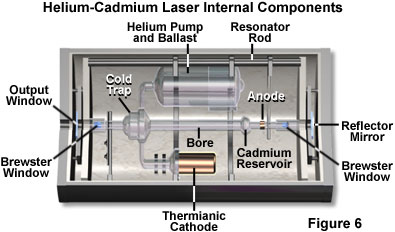
Helium-cadmium lasers (illustrated in Figure 6) are considered to be a member of the helium-neon family, and represent an economical source for continuous-wave output in the ultraviolet (325 nanometers at 75 milliwatts and 353 at 20 milliwatts) and violet (442 nanometers at 200 milliwatts) spectral regions. These lasers rely on cadmium vapor as a lasing medium, which is distributed uniformly throughout the bore from the heated cadmium reservoir (at approximately 250 degrees Celsius) by gas-phase electrophoresis. The helium pump maintains a constant helium pressure, which is about a thousand times higher than that of the cadmium vapor. Helium-cadmium lasers display more beam noise than their helium-neon counterparts, primarily because of localized fluctuations in metallic cadmium vapor concentrations in the bore. They also have a shorter lifespan, typically around 5,000 operating hours.
One group of investigators has described the use of a ratio-imaging confocal microscope coupled to both an argon laser operating at 488 nanometers and a helium-cadmium laser emitting at 442 nanometers. This system allowed the group to measure the intensity ratio from the pH-sensitive dye BCECF [having an IUPAC name of 2',7'-bis-(2-carboxyethyl)-5-(and-6-)-carboxyfluorescein] in isolated renal tubules. Similar measurements have been made utilizing the 458-nanometer line of the argon laser in both widefield and confocal microscopy systems. Another researcher reported using the 325-nanometer output of a helium-cadmium laser to excite two dyes simultaneously and perform emission ratio imaging.
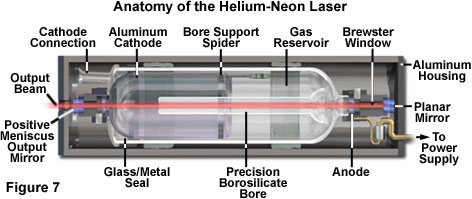
Helium-neon lasers are the most widely utilized laser systems for a broad range of biomedical and industrial applications, and display the most superior Gaussian beam quality of any laser. These lasers are readily available at relatively low cost, have compact size dimensions, and exhibit a long operating life (often reaching 40,000 to 50,000 hours). The low power requirements, superior beam quality (virtually a pure Gaussian profile), and simple cooling requirements (convection) make helium-neon lasers the choice system for many confocal microscopes.
Presented in Figure 7 is a cut-away diagram of a typical helium-neon laser system, which is constructed of glass with a large oxidized-aluminum cold cathode as the electron emitter. Operating in the abnormal glow current density gas discharge region, helium-neon lasers are generally high-voltage and low current systems, with discharge currents being limited to a few milliamperes and potentials ranging from several hundred to a thousand volts. Progressive deterioration of the oxide coating on the cathode, which ultimately leads to sputtering of aluminum, is the limiting factor in helium-neon laser operating life. Large-diameter discharge tubes typically have longer life spans than smaller tubes (40,000 hours versus about 10,000 hours, respectively).
The nitrogen laser has been in use for a number of years as a pulsed light source for both spectroscopy and microscopy. The output is confined to a single line, having a 337.1-nanometer wavelength, with pulse durations ranging from picoseconds to nanoseconds. The pulse repetition rate can be as high as 200 pulses per second. Nitrogen lasers can also be employed to pump dye molecules for longer-wavelength emission. In addition, these lasers have been utilized as a light source for high-speed calcium ratio imaging using the ultraviolet-excitable dye Fura-2. In this application, two lasers are used; one serves as a direct source of 337-nanometer light, and the other is dye-pumped to produce emission at 380 nanometers. Pulsing each laser at a repetition rate of 15 per second, in synchrony with the video rate, produces a ratio image every 66 milliseconds.
Diode lasers, semiconductor devices that have been under development for decades, are now available with sufficient output power to be of interest to microscopists. The most common of these devices operates in the near infrared, but diode lasers operating in the red and blue regions (and recently, other wavelengths), with substantial output power, have been developed. In addition, those diode lasers now available exhibit improved beam shape and stability, allowing them to replace helium-neon lasers in many applications. Diode lasers typically have a lifespan ranging between 10,000 and 50,000 hours, but are extremely sensitive to electrostatic shock, so they must be handled carefully.
Of great interest to optical microscopists is the development of tunable diode lasers, which can now compete in terms of power and versatility with tunable dye lasers and Ti:sapphire lasers (discussed below and illustrated in Figure 1). Tunable dye lasers have a wavelength range of 600 to 1800 nanometers and can deliver 5 to 25 milliwatts of power. They have the advantages of relatively low cost, compact size, long lifetime, and low heat production, eliminating the requirement for external cooling systems.
Diode-pumped solid-state lasers (DPSS) utilize a diode laser instead of noble gases, arc lamps, or flashlamps to pump the solid-state lasing material. The power output, beam quality, and stability exhibited by diode-pumped lasers approaches that of a gas (helium-neon) laser, but the efficiency and size are more comparable with diode lasers. Typical operating and maintenance costs of diode-pumped lasers is less than that of gas lasers, and most systems are cooled either by convection or forced air.
Diode-pumped neodymium-yttrium aluminum garnet (Nd:YAG) lasers generate 1064-nanometer light in the milliwatt power range. Frequency doubling leads to a compact device with a continuous-wave output at 532 nanometers, and frequency tripling can also be employed to generate a pulsed output at 355 nanometers. The tightly folded resonator (TFR) was developed for pumping a crystal of neodymium-yttrium lithium fluoride (Nd:YLF) with high power and efficiency using an array of diode lasers to generate several watts of power at 1047 nanometers. Frequency doubling, tripling, and quadrupling in this type of laser results in power outputs up to hundreds of milliwatts of coherent light at 523, 349, and 262 nanometers (second, third, and fourth harmonics). Other advantages of diode lasers as pump sources include an extended lifetime (typically more than 5000 hours, compared to a few hundred hours for lamps), a collimated and easily focused output that matches the small lasing volume of the solid-state laser, and greatly reduced thermal loading of the laser rod, which usually requires water cooling when halogen arc lamps are used as pumps.
Development of diode-pumped solid-state lasers has been driven by industrial and commercial applications requiring high power (generally several watts) in the green (532 or 523 nanometers) and ultraviolet (355 or 349 nanometers, and the fourth harmonic at 266 nanometers) wavelength ranges. Output in the ultraviolet spectral region is pulsed, with energies ranging from 100 microjoules to 10 millijoules, pulse durations in the nanosecond range, and repetition rates as high as 10 kHz. These lasers are very useful in microscopy for triggering the release of caged compounds. The pulse repetition rates, however, are still too slow for use as an illumination source for most confocal microscopy applications.
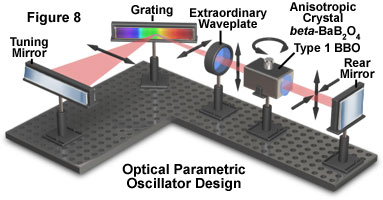
Further development has led to the combination of diode-pumped solid-state lasers with optical parametric oscillators (OPOs; see Figure 8) to produce a tunable, pulsed output that is continuously variable from 205 nanometers to 2000 nanometers. Although the initially-available systems have been expensive and complex in operation, scaled-down versions more suitable for use in microscopy are being introduced.
Titanium-doped sapphire lasers (commonly known as Ti:sapphire lasers, see Figure 1) provide the advantages of tunability for pulsed and continuous light delivery, as well as solid-state dependability. These lasers can deliver very short light pulses (approximately 80 to 100 femtoseconds) at high repetition rates (100MHz). The range of tunable wavelengths extends from the far red to the near-infrared spectral regions (700 to 1000 nanometers). Most of these lasers are operated with optical pumping by high-power argon lasers, as well as requiring water cooling. As a result of the expense and complexity involved with operating and maintaining Ti:sapphire lasers, their use has been limited primarily to multiphoton microscopy in relatively few laboratories.
Recently, a diode-pumped Cr:LiSAF (chromium-doped lithium strontium aluminum fluoride) laser has been developed that delivers high-frequency 90 femtosecond pulses at a wavelength of 860 nanometers, and an average output power of 88 milliwatts. The small size and low power requirements of the Cr:LiSAF laser make it an attractive light source for multiphoton fluorescence microscopy in place of the Ti:sapphire laser.
Conclusions
Among the major differences between multiphoton and confocal laser fluorescence microscopy is the type of laser utilized in these often complementary techniques. Lasers for multiphoton microscopy are considerably more expensive and difficult to operate than the small air-cooled lasers employed in confocal microscopy.
Development of user-friendly turnkey laser sources for multiphoton microscopy is a necessity if the technique is destined to enjoy widespread acceptance. To date, the scope of multiphoton investigations is limited by the restricted choice of excitation wavelengths provided by suitable laser illumination sources. In order to alleviate complex laser daily maintenance schedules and expand the spectrum of useful excitation wavelengths, new developments in femtosecond-duration optical pulse lasers are essential. Specifically, new laser sources must be engineered that are wavelength-tunable throughout the upper visible (500+ nanometers) and near-infrared portions of the spectrum.
During the past ten years, many new short-pulse laser system variations were made possible by the discovery of Kerr-lens mode locking in titanium-doped sapphire crystal lasers. Other new systems, such as diode-pumped solid-state and single-mode fiber femtosecond lasers are being investigated for their potential as excitation sources for multiphoton microscopy. In the future, frequency doubling of femtosecond pulsed lasers by optical parametric oscillators (OPOs) may provide a universal solution to cover the useful wavelength range.
Present applications of lasers in microscopy are expanding rapidly in the areas of confocal microscopy, optical trapping, and the release of caged compounds and fluorophores. The development of compact solid-state lasers with emission lines in the blue-green and ultraviolet regions of the spectrum should serve to further increase the utilization of these devices in microscopy.