빛의 회절
회절이란 미립자와 상호 작용하는 파동 현상을 정의하는 용어입니다. 여기서 광파의 회절에 대해 회절의 예시부터 빛의 회절 방정식까지 다루어 보겠습니다.
회절의 정의
일반적으로 빛은 항상 직선으로 나아간다고 알고 있지만, 광파는 장벽 근처를 통과할 때 장벽 주위에서 휘어져 퍼져나가는 경향이 있습니다. 회절은 장애물을 통과하거나 지날 때 파동이 확산된다는 의미입니다. 빛에 적용하여 더 자세히 말하자면, 빛의 파동이 빛의 파장과 물리적으로 크기가 거의 같거나 심지어 그보다 더 작은 모퉁이, 틈 또는 구멍을 지나갈 때 빛이 회절됩니다.
회절의 예시
파동의 회절은 광원 앞에 손을 대고 천천히 손가락 두개를 접어 그 사이에 빛이 투과하는 것을 관찰하는 것으로 아주 간단하게 시연할 수 있습니다. 손가락이 서로 다가가고 서로 아주 가까워질수록 손가락과 평행한 일련의 검은 선이 보이기 시작할 것입니다. 이 평행한 선이 바로 회절 패턴입니다. 이 현상은 빛이 빛의 파장과 같은 크기의 미립자 주변에서 ‘굴절’할 때도 발생할 수 있습니다. 이러한 현상의 좋은 예시는 우리가 종종 한 줄기 희망에 비유하듯이 구름 사이로 햇빛이 회절되는 모습입니다. 그림 1에 보이는 바다 위의 아름다운 노을로 확인할 수 있습니다.
빛이 구름 속 물방울에서 회절될 때, 구름이 파란색, 분홍색, 보라색 및 초록색의 파스텔 색상으로 변하는 것을 종종 관찰할 수 있습니다. 회절의 양은 빛의 파장에 따라 다르며, 짧은 파장은 긴 파장보다 더 큰 각도로 회절됩니다(사실상 파란색과 보라색 빛은 붉은색 빛보다 더 큰 각도로 회절된 것입니다). 빛의 파동이 공기 중으로 이동하다가 물방울과 만나면 그림 2와 같이 물 대비 공기의 접점에서 처음 굴절되며, 다시 접점을 맞닥뜨리면서 반사됩니다. 여전히 물방울 안을 지나가는 빛줄기는 접점에 세 번째로 부딪히며 다시 한 번 굴절됩니다. 이 접점과의 마지막 접촉은 빛을 공기 중으로 굴절시키지만 다음 그림과 같이 빛의 일부가 회절되기도 합니다. 이 회절 요소는 빛의 밝은 고리가 관찰자 머리의 그림자를 둘러싸는 첼리니의 후광(또한 하일리겐샤인 효과로도 알려짐)이라고 부르는 현상으로 이어집니다.

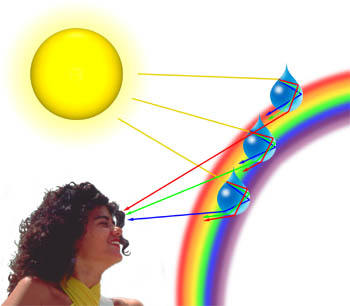
그림 2
회절과 산란의 차이점
회절과 산란이라는 용어는 종종 번갈아 사용되고 거의 동의어로 여겨집니다. 회절은 특별한 빛의 산란을 의미하며, 이는 규칙적으로 반복되는 특징이 있는 물체(예: 회절 격자)가 회절 패턴으로 일정하게 빛의 회절을 생성하는 경우입니다. 실제로 대다수의 물체는 모양이 매우 복잡하고 무작위의 빛의 산란을 집합적으로 생성할 수 있는 여러 개별적인 회절 특질로 이루어져 있다고 간주됩니다.
단일 슬릿 광학 회절 실험
광파의 회절과 관련한 고전적이고 가장 기본적인 개념으로는 19세기 초반에 처음 이루어진 단일 슬릿 광학 회절 실험이 있습니다. 광파가 슬릿(또는 조리개)을 통해 전파될 때, 그 결과는 입사 선속의 파장에 대한 조리개의 물리적 크기에 따라 달라집니다. 이 현상은 그림 3에서 설명됩니다. 레이저에서 발생하며 빛과 유사한 점광원 S에서 방출된 일정한 단색파가 조리개 d를 통과하여 P 지점에 떨어지는 초기 입사 광속과 Q 지점의 최초 부수적 최대치와 함께 회절한다고 가정한 것입니다.
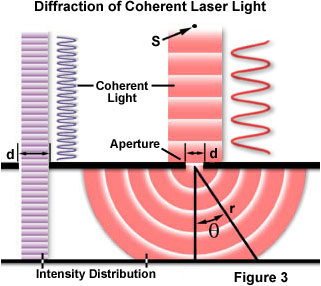
그림의 좌측에서 확인할 수 있듯이, 파장(λ)이 조리개 넓이(d)보다 훨씬 작으면 파동은 미립자 또는 조리개가 없을 때 그저 직선으로 나아갑니다. 하지만 파장이 조리개의 크기보다 크면 다음 공식에 따른 빛의 회절이 발생합니다.
sinθ = λ/d
θ는 중앙 입사 전파 방향과 회절 패턴의 첫 최솟값 사이의 각도입니다. 중심에서 거리가 멀어질수록 연속적인 부수적 최댓값의 강도가 감소하면서, 이 실험은 부수적인 최대치 양 측면에 위치한 밝은 중앙의 최댓값을 생성합니다. 그림 4는 빔 강도 대비 회절 반경으로 이를 설명합니다. 부수적인 최댓값 사이에 발생하는 최소치는 π 배수에 위치한다는 점을 유의하십시오.
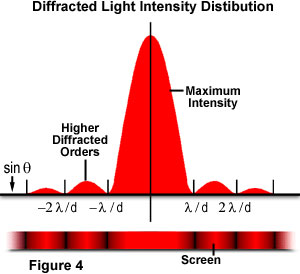
이 실험은 빛이 파동으로 이동한다는 중요한 증거를 제시한 Augustin Fresnel과 Thomas Young에 의해 처음 설명되었습니다. 지점 L에서 방출된 일정한 단색파(예를 들어 레이저 조명)가 조리개 d로 얼마나 회절되는지 상기 이미지에서 확인할 수 있습니다. Fresnel은 지점 Q(εQ로 지정됨)의 1차 최댓값의 진폭이 다음과 같은 방정식일 것이라고 가정했습니다.
dεQ = α(A/r)f(χ)d
여기서 A는 입사파의 진폭이고, r은 d 와 Q 사이의 거리이며, f(χ)는 χ의 함수로, Fresnel이 고안한 기울기 인수입니다.
빛의 회절
좁은 슬릿 또는 조리개를 통과할 때 빛의 빔이 회절되는 방식을 알아봅시다. 파장과 조리개 크기를 조절하여 회절 입사 패턴에 어떤 영향을 미치는지 관찰하십시오.
빛의 회절은 광학 기기의 해상력을 제한하는 중요한 역할을 합니다(예: 카메라, 쌍안경, 망원경, 현미경, 안구 등). 해상력은 인접한 두 지점의 개별 이미지를 생성하는 광학 기기의 기능입니다. 이는 종종 기기의 렌즈 및 거울 품질과 주변 매체(주로 공기)의 특성에 따라 결정됩니다. 파동과 같은 자연광은 모든 광학 기기의 해상력을 궁극적인 한계에 맞닥뜨리게 합니다.
원형 조리개 회절 방정식
회절을 설명할 때는 빛이 회절되는 조리개로 슬릿을 사용했습니다. 하지만 모든 광학 기기는 원형 조리개를 사용하며, 안구의 동공 또는 현미경의 원형 조리개 및 렌즈를 그 예로 들 수 있습니다. 원형 조리개는 패턴이 자연적으로 원형 대칭을 나타낼 때를 제외하고 상기 설명과 비슷한 방식으로 회절 패턴을 생성합니다. 원형 조리개에 의해 생성된 회절 패턴의 수학적 분석은 다음의 회절 방정식으로 설명합니다.
sinθ(1) = 1.22(λ/d)
여기서 θ(1)은 1차 회절 최소치(첫번째 어두운 링)의 각 위치이고, λ는 입사 광선의 파장이고, d 는 조리개의 지름이며, 1.22는 상수입니다. 대부분의 환경에서 각도 θ(1)은 매우 작기 때문에 각도의 sin 및 tan와 거의 동일한 근사치로 산출됩니다.
θ(1) ≅ 1.22(λ/d)
이러한 공식에서 최대값은 더 긴 파장과 더 작은 조리개로 더욱 넓게 퍼져, 중앙 최대값이 λ/d,와 정비례합니다. 회절의 부수적인 최소치는 렌즈에 의한 내재적인 빛의 회절로 인해 광학 현미경의 대물 렌즈에 유용한 배율로 제한을 둡니다. 렌즈가 아무리 완벽하더라도 렌즈에 의해 생성된 이미지의 점화원은 부수적이고 더 높은 최대치가 수반됩니다. 이는 렌즈 직경이 무한대일 때만 제거할 수 있습니다. Θ(1)보다 적은 거리만큼 떨어진 두 물체는 배율이 아무리 높더라도 해상할 수 없습니다. 이러한 방정식은 조리개로부터 무한히 먼 거리의 점화원 이미지에서 파생되었지만, d가 대물 렌즈의 직경으로 대체되었을 때 망원경의 해상력을 합리적으로 추론합니다.
따라서 두개의 사물이 거리 D를 두고 각각 떨어져 있고 관찰자와는 거리 L을 두고 있는 경우, 그 사이의 각도는 다음과 같습니다.
θ = D / L
산출할 두개의 마지막 방정식을 다음과 같이 요약할 수 있습니다.
D(0) = 1.22(λL/d)
여기서 D(0)는 해상할 수 있는 사물 간의 최소 이격 거리입니다. 이 회절 공식을 이용하면 사람의 눈은 0.056 밀리미터 떨어진 사물을 해상할 수 있지만, 망막의 광수용체는 이 정도의 해상도를 허용할 만큼 충분히 가까지 붙어있지 않으며, 일반적인 환경에서는 0.1 밀리미터가 더 현실적이라고 볼 수 있습니다.
광학 현미경의 해상력은 앞서 언급한 것들을 포함한 다수의 요인으로 결정되지만, 가장 이상적인 환경에서는 약 0.2 마이크로미터입니다. 이는 망원경의 광학 정렬, 렌즈의 품질을 비롯하여 표본을 이미징하는 우세한 빛의 파장을 고려한 수치입니다. 보통 각 대물렌즈의 정확한 해상력을 계산할 필요는 없지만(대개 시간 낭비), 현미경 렌즈의 기량은 실생활에 적용되기 때문에 이해하는 것이 중요합니다.
Sorry, this page is not
available in your country.